I first met John McKay in Cambridge in 1980 (if I remember correctly), and last met him in Edinburgh in 2004. We occasionally corresponded by email over the years, but this correspondence has now come to end, since he recently died. But this isn’t the McKay correspondence I want to talk about.
McKay was famous for his crazy ideas. He specialised in ideas that were so crazy, that they had to be true, because you just couldn’t make it up. The most famous is the idea that 196884 = 196883 + 1, an idea so outlandish that no-one took it seriously to begin with, but an idea that links two previously unconnected areas of mathematics, and has spawned a wealth of new mathematics. Yet it still goes by the name of “Monstrous Moonshine”, which gives you an idea of what a ridiculous and stupid crackpot idea it was originally considered to be.
Another of his crazy ideas was that if you take the extended E_8 Dynkin diagram, consisting of 8 nodes joined in a straight line plus another joined to the 6th in the row, and label the nodes 1,2,3,4,5,6,4,2 along the line, and 3 for the extra node, which is a reasonably natural thing to do, then these numbers are the degrees of the (irreducible complex) representations of the binary icosahedral group. They are also the orders of the products of two 6-transpositions in the Monster. Crackpot, or deeply significant?
Deeply significant, of course. The three objects here: the icosahedron, E_8 and the Monster, are the largest exceptional objects in their respective domains of mathematics, and the connections between them are a sign of the deep unity of mathematics, at a level we still cannot really comprehend. I’m not going to talk here about the Monster connections, which have led some physicists off into a wild goose chase, but about E_8 and the icosahedron.
This McKay correspondence enables me to translate backwards and forwards between a discrete fundamental theory of quantum physics, based on the icosahedron, and a continuous quantum field theory, based on E_8. As each theory tells us something that the other does not, between them they can solve all the fundamental problems. Let me first refine the notation so that we distinguish representations 1a, 2a, 3a, 4b, 5a, 6a, 4a, 2b along the line, and 3b for the extra node. Alternate nodes are bosonic (1a, 3a, 5a, 4a, 3b) and fermionic (2a, 4b, 6, 2b). The first 6 nodes are the symmetric powers (0, 1, 2, 3, 4, 5) of 2a. The 6th symmetric power is 3b+4a, and the 7th is 2b+6a.
Now every reasonable model of physics is obtained by deleting some nodes from this diagram. The Standard Model of Particle Physics, for example, appears if you delete 2a, 4b, 5a and 6a. Penrose twistors appear if you reinstate 2a. The Georgi-Glashow SU(5) theory appears if you reinstate 6a, and if you add in 5a as well you get the SO(10) theory. The paper I recently finished (see the previous post) describes what happens if you combine these theories by adding in either 2a, 5a and 6a to get a Georgi-Penrose model, or 2a, 4b and 6a to get a supersymmetric model.
At this point I can see what I did wrong. The correct way to look at the model is to add in 2a, 4b and 5a, and leave out 6a instead. Now we have a Grand Unified Theory with gauge algebra su(2,4) + su(2) + su(3), where su(2)+su(3) describes all the nuclear forces, and su(2,4) describes everything else, that is electromagnetism and gravity. If we restrict from su(2,4) to the Lorentz algebra so(1,3), then the gauge algebra acquires extra terms su(2) + u(1) + so(1,1). Here the second copy of su(2) is Woit’s chiral gravity gauge algebra, and u(1) is the gauge algebra for electromagnetism, while so(1,1) is the mass gauge algebra, that explains how mass works.
So now I should be able to explain how mass works, and why the proton/electron mass ratio is 1836.15, and not some other equally stupid number. First of all, it is now obvious that this mass ratio is not a universal constant, but depends on the choice of Lorentz gauge. It is now obvious that this choice was made in 1973, when the standard model was adopted. It is now obvious that the standard Lorentz gauge is stuck in a time warp back in 1973, and no longer corresponds exactly to the Lorentz gauge applicable to the Large Hadron Collider in 2022. It is now obvious that if we re-calibrated the whole of physics from scratch, with a new choice of Lorentz gauge applicable to the laboratory today, we would be forced to conclude that the proton/electron mass ratio is 1836.45, not 1836.15.
This idea is, of course, completely and utterly crazy. It is such a crackpot idea that it must be true. You just couldn’t make it up.
I would like to dedicate this post to the memory of John McKay, who taught me how to go beyond crackpottery to find the ultimate truth.
October 29, 2022 at 9:07 am |
Oh, I forgot to tell you the name of this new domain of physics that I have invented: it is called “Ludicrous Lunacy”. One day this epithet will be as well-known as “Monstrous Moonshine”, if not more so.
November 6, 2022 at 8:35 am |
On second thoughts, I think “Lorentzian lunacy” might be better: the central idea being that the precise identification of the two copies of the Lorentz group (the Einstein and Dirac versions) depends (very slightly) on the phase of the Moon, or at least on fundamental parameters of the Moon’s orbit.
October 29, 2022 at 9:23 am |
I’ve told you about the pions in the sky, haven’t I? The pion mass ratio is to a first approximation 1 + 1/(no. of days in a lunar month). Is this pie in the sky, or lunacy, or both?
But what does it mean? It means that the tidal effects of the (quantum) gravity of the Moon on the nucleus of a single atom not only *can* be detected, but *have been* detected.
October 29, 2022 at 4:57 pm |
Lunacy in the Sky with Pions. LSP.
October 29, 2022 at 5:04 pm
LOL
October 29, 2022 at 5:40 pm
Better, I suppose, than Lunacy in the Sky with Dark matter (LSD), which seems to be what most physicists are on.
October 29, 2022 at 7:18 pm |
Of course, the Sun has tidal effects as well – for those, look no further than the kaons. Just remember that you cannot have your kaon and eat it. And remember the CP (Cake Partition) violation – if you separate your kaon cake into the short-lived eigenstate (which you eat) and the long-lived eigenstate (which you keep), there will also be some short-lived crumbs, caused by the mixing of electromagnetism (which sticks the crumbs to the cake) and gravity (which causes them to fall off).
October 29, 2022 at 8:15 pm |
The new decomposition of E8 is neat. And I have a question about the three neutrino-gravitons: do they correspond in any way to different spatial directions?
But I still don’t see how a “new choice of Lorentz gauge” would change the measured proton/electron mass ratio.
October 29, 2022 at 9:51 pm |
Well, it’s early days, and I can’t actually answer these questions yet. It is necessary to get a quite explicit quantum gravity first. I am therefore relying on the experimental evidence more than the (future) theory. The 3 sigma discrepancies between experimental measurements of the p/e mass ratio analysed in the 1969 NIST evaluation of fundamental constants disappeared in 1973, at exactly the same time that the underlying theory was replaced by a new theory. To me, this is a suspicious indication that the underlying problem may have been evaded rather than solved.
Your first question, I suppose, relates to how the directions in space transform under SU(2,4). This is a difficult question, because the standard quantum mechanical Lorentz group SL(2,C) embeds in SU(2,2), which commutes with the gauge group U(2), but SU(2,4) also contains SO(2,4), which is isomorphic to SU(2,2)/Z_2. Therefore there are two distinct types of Lorentz group with completely different properties. This is analogous to the existence of both SL(2,C) and SO(3,1) in SL(4,R), and the fact that standard physics does not make a consistent choice of a single “Lorentz group”. Some authors do indeed distinguish between a “spacetime” SO(3,1) and a “spin” SL(2,C), but this is rare, and it is always assumed that they commute with each either, which I believe is incorrect.
In other words, there is a complicated relationship between “directions” defined by SL(2,C), and “directions” defined by SO(3,1). This is where we have to look for answers to difficult questions about relationships between internal symmetries (neutrino generations) and external symmetries (momentum directions and gravitational field directions), not to mention photon polarisation.
Your second question is about the mass gauge. For this it may be sufficient to work in SU(2,2) rather than SU(2,4), since SU(2,2) contains SL(2,C), commuting with a copy of the real numbers. If you change your copy of SL(2,C), then you change your copy of the real numbers that you use to measure mass. Therefore all the masses shift around, because there is no simple relationship between these two copies of the real numbers. Since there is an 8-parameter family of such mass gauges, there may be as many as 8 independent and apparently arbitrary masses.
And finally to the difference between gravitational and inertial mass, which is the difference between the mass gauge inside SO(2,4) and the mass gauge in SU(2,2). Since these groups do not have the simple relationship that is usually assumed, there is no simple relationship between gravitational mass and inertial mass.
October 29, 2022 at 10:05 pm |
Incidentally, the embedding of SO(2,4) in SU(2,4) provides a tantalising glimpse of the Riemann Curvature Tensor: the 20 dimensions of SU(2,4)/SO(2,4) can be obtained from the 6-dimensional representation of SO(2,4) by taking the symmetric square and discarding the scalar (metric). But I don’t see how we can identify the 6-dimensional representation with the anti-symmetric square of Minkowski spacetime, so I don’t see how we can identify these 20 parameters with curvature of spacetime. Nevertheless, they *are* parameters of quantum gravity.
October 29, 2022 at 11:31 pm
This interests me because I tried to find a geometric meaning of SU(2,4), and failed. Are you saying that SU(2,4) acts naturally on, what, the cube of the 6-dimensional representation of SO(2,4)?
October 31, 2022 at 4:20 am
In https://doi.org/10.1215/kjm/1250281656, I read that SU(p,q) is “the conformal CR automorphism group” of a particular “projective hyperquadric”, CR geometry being a study of real submanifolds of complex manifolds.
I had hoped that SU(2,4) might have a natural action on the Riemann curvature tensor, if the latter is expressed in terms of twistorial variables.
And I would still like to know if SU(2,4) can be expressed e.g. as a particular quotient of SO(2,4)^3. That would be a encouraging indication that you can indeed build an SU(2,4) invariant out of twistors.
October 31, 2022 at 8:17 am
I don’t know what it means to express SU(2,4) as a quotient of SO(2,4)^3. It certainly cannot be done with group theory, but perhaps you mean something more geometrical. In any case, I can’t answer that question.
As for the Riemann Curvature Tensor, there may be more than one possibility for embedding it in this model. My first suggestion (above) is that it lies in the 20 (real) dimensions of SU(2,4) complementary to SO(2,4). There is another possibility that it lies in the 40 dimensions of the symmetric cube of the 6-rep. This second possibility makes it 20-dim real or 10-dim complex for SO(2,4), and 10-dim quaternionic for SU(2,4). Then SU(2,4) could be said to act on two copies of the Riemann Curvature Tensor.
At the same time, it means that the RCT is a property of leptons, not quarks, and implies that it is a correction to ordinary gravity for the quantum properties of electrons. This is at least physically plausible, and means that neutrino oscillations are the quantum effect by which the RCT arises macroscopically. But it doesn’t work mathematically, because on restriction to SO(1,3) the representation looks nothing like the 1+9+complex 5 of the RCT. So if true, this means the RCT cannot be more than a first-order approximation to the truth. This is also physically plausible, given the experimental evidence for MOND over GR.
October 31, 2022 at 3:42 pm
“I don’t know what it means to express SU(2,4) as a quotient of SO(2,4)^3”
I was trying to guess what this means:
“the 20 dimensions of SU(2,4)/SO(2,4) can be obtained from the 6-dimensional representation of SO(2,4) by taking the symmetric square and discarding the scalar”
I’m assuming this isn’t just numerology based on two things each having 20 degrees of freedom, and that there’s some kind of rigorous group-theoretic proposition here, but I haven’t figured out what it is.
October 31, 2022 at 4:23 pm
Oh I see. In the split signature, adjoint SL(6.R) consists of all traceless 6×6 matrices, and SO(6) consist of the anti-symmetric ones, leaving the traceless symmetric ones for this 20-dimensional rep. Here we just do the same thing in the SU(2,4) signature. I haven’t bothered to specify exactly what the matrices are, but just used the abstract representation theory at this point. Since the adjoint representations are real whatever the signature, we know we can fill in the details later if/when necessary.
October 30, 2022 at 8:28 am |
I don’t really know yet. Maybe I will also fail to find a geometrical meaning for SU(2,4). But there are lots of clues, so I just have to get to work and see what happens. The biggest clue, I think, is that all E8 models, as far as I can see, have failed to identify the handedness of the weak force with the handedness of the Lorentz group in a satisfactory way. Perhaps this is really what Distler and Garibaldi meant when they said there is no chiral theory in E8. But what I take it to mean is that these two sorts of handedness are actually *not* the same in physical reality. The Standard Model forces them to be the same by the kludge of projecting with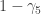 , but this does violence to both the mathematics and the physics.
, but this does violence to both the mathematics and the physics.
So this new model separates the concepts of LH and RH spin from the concepts of LH and RH isospin, and uses all four combinations. Now the RH isospin leptons lie in adjoint SU(2,4), while the LH isospin leptons lie in the anti-symmetric cube of the natural 6-dimensional representation. Both behave as a pair of twistors under SU(2,2), but are completely different under SO(2,4), which associates bosons to them. That means they react to different forces, or to the same force in different ways. I don’t yet understand how this works, but it is quite clear that beta decay and muon decay should be regarded as separate forces, not just different aspects of the weak force.
Anyway, the SU(2,4) representations that I need to understand are (1) the adjoint, where the RH isospin leptons live, (2) the natural 6-dimensional complex representation, where the LH isospin quarks live, (3) its anti-symmetric square, 15-dimensional complex, where the RH isospin quarks live, and (4) its anti-symmetric cube, 10-dimensional quaternionic, where the LH isospin leptons live. The restrictions to SU(2,2) x SU(2) x U(1) give the standard model, for three generations, as was already demonstrated in the previous paper. My hope is that the restriction to SO(2,4) will give a passable imitation of general relativity. If this works out, then we can start to see how unification might work.
At any rate (1) seems to imitate the Riemann Curvature Tensor, while (2) is the domain of protons and neutrons, which dominate the mass budget for ordinary matter, and also of Minkowski spacetime, so this may explain the metric as being derived from the large-scale structure of matter. Then (3) is an anti-symmetric tensor (i.e. a force) on baryons, and splits for SO(1,3) x SO(1,1) as 1 + 6 +8, thereby separating 6 for EM from 1+8 for something like the Einstein Tensor. Finally (4) splits as 4+4+12, containing spacetime, its dual, and chemistry.
But spacetime appears in both (2) and (4), so that leptons and quarks experience spacetime differently. Therefore we also experience spacetime differently, when the balance of power between leptons and quarks changes. Or maybe we don’t – maybe only an external observer can detect this change?
October 31, 2022 at 9:04 am |
I’ve tried again (above) to answer your RCT questions. Here I would like to comment on the action of SO(2,4) on RH isospin particles. It acts on half the RH leptons and all the RH quarks in its adjoint (anti-symmetric 2-tensor) representation. It acts on the other half of the RH leptons in its symmetric 2-tensor (20=21-1) representation. This makes a very clear distinction between RH electrons (which are presumably particles) and RH neutrinos (which are presumably symmetries, not particles).
So what are these weird symmetries? They are conformal symmetries, that mix linear motion with circular motion, and explain how the Lorentz transformations of linear motion convert to transformations (in particular of mass) due to rotations. But in particle physics they mix fermions with bosons, so how can this be? I don’t suppose experiment really can tell us anything about whether RH quarks mix with gluons or not, so I’m not too bothered about that. And I’m not going to get involved in any discussion about the experimental properties of hypothetical RH sterile neutrinos! So that leaves only the RH electrons to worry about.
Now which representation tells us about RH electrons? Are they symmetric or anti-symmetric tensors? I think they must be symmetric. On restriction to SO(1,3) this tensor breaks up as 1+9+1+4+1+4, compared to 1+9+ complex 5 for the RCT. So we can still use the 9 for the Einstein Tensor, but the Weyl Tensor (complex 5) disappears entirely, to be replaced by a pair of vectors. Hence the spin 2 graviton disappears entirely (in agreement with experiment), to be replaced by something even more weird and inexplicable. (There is another theory that this has already happened.)
In other words, instead of spin 2, this model has spin 0 + (1/2,1/2). Spin 0 might be a Higgs boson, but spin (1/2,1/2) clearly falls apart into spin (1/2,0) neutrinos and spin (0,1/2) anti-neutrinos. Therefore, as I’ve been saying for years, neutrinos *are* gravitational waves.
October 31, 2022 at 9:18 am |
So I guess I’ve come back to the point of view that the whole of SU(2,4) can be thought of as a gauge group for quantum electro-gravity, breaking up as conformal SO(2,4) plus the (corrected!) RCT. Pretty neat, eh?
October 30, 2022 at 6:38 pm |
The last emails I had from McKay were in 2016, and indicate that he was still actively looking for unexpected connections between different parts of mathematics at that time.
October 31, 2022 at 12:10 pm |
I have been asked where the tidal effects of gravity go, if I have no spin 2 graviton. This question is supposed to be a definitive refutation of my model. It is not: it only exposes a woeful lack of understanding of what tides actually are.
In fact, this is an easy question to answer: tidal effects lie in the Einstein Tensor, *not* in the Weyl Tensor. The Weyl Tensor is about gravitational waves, not about tides. Tides are *matter* waves, not *gravitational* waves. They are only spin 2 in non-relativistic gravity. In relativistic gravity, they have spin (1,1).
October 31, 2022 at 1:15 pm |
I already discussed the tidal effects of the Moon’s gravity on the atomic nucleus in an earlier comment. These effects are mediated by pions, 3 particles of spin 0. The fact that there are three of them is encoded in the spin 1 part of the spin (1,1) representation. But if you really want spin 2 tides, you want the kaons, of which there are 5 (the SM only has 4, but 5 is what experiment says). The singleton is the eta meson, of course.
The pion mass ratio is a mapping from the spin 1 representation to the spin 0 representation, that picks out the rotation of the Moon in its orbit as the defining property. The kaon mass ratio describes the relationship of the two charged kaons to the three neutral kaons, and is a mapping from the spin 2 representation to the spin 0 representation, which picks out the inclination of this orbit as the defining property. In other words, it relates the lunar tides to the solar tides.
October 31, 2022 at 2:59 pm |
To put it another way, gravitational waves are eddies in the fabric of spacetime. You can’t hitch a ride on them, as Ford Prefect maintained. “The Hitchhiker’s Guide to the Galaxy” is a work of fiction, not an explanation of the relationship between gravitational waves and tides. Arthur Dent had a very sane, down-to-Earth response: “Is he?” And in fact, rather than fiction, the answer to that question is “Yes.” Some physicists seem to take the HHGG as a textbook for beyond-the-standard-model physics. I don’t think that is a sane approach.
October 31, 2022 at 3:28 pm |
The most important point is to include the 5a representation, because without it you can’t quantise the tides. At the quantum level, this node of the Dynkin diagram corresponds to SU(2)_R, acting on leptons to reduce them to the lowest (gravitational) mass eigenstate.
November 4, 2022 at 9:42 pm |
I was tied up for a few days… thanks for explaining about the embedding of SO in SU.
Continuing to plod ahead regarding SU(2,4), SO(2,4) and the Riemann curvature tensor… One way to approach this, is in terms of extending the conformal group. That is, we will start with a geometry (like twistor geometry) where SO(2,4) conformal transformations are meaningful, and then we want to find a meaning for the rest of SU(2,4) too.
In this regard, it’s significant that part, but only part, of the Riemann curvature tensor, is invariant under conformal transformations (namely, the Weyl tensor). One has to decide whether this will continue to be so, in the sought-after geometry based on SU(2,4).
November 4, 2022 at 10:29 pm |
I’ve been working out some details of how SU(2,2) and SO(2,4) differ inside SU(2,4), and it’s looking really interesting – although it’s hard to explain without going into technicalities. Both SU(2,2) and SO(2,4) contain effective definitions of mass, but they are different definitions. I take the former as inertial mass – defined by the Dirac equation – and the latter as (active) gravitational mass. Then the gravitational mass has an extra term which lies in an imaginary momentum direction – I take this to mean angular momentum or spin. Therefore if the direction of rotation of the experiment relative to an inertial frame (of the Solar System, say, for the sake of argument) changes, then the relationship between passive inertial and active gravitational mass can change. Since the direction of the Earth’s axis relative to the Solar System rest frame does indeed change slowly over time, one can now start to make predictions for how gravitational mass changes relative to inertial mass. In particular, my prediction is that while the inertial mass ratio of proton to electron remains constant (in the context of the standard model) at 1836.15…, the gravitational mass ratio has drifted since 1973 to a value around 1836.45 today. This difference of .02% is well within the scatter of recent measurements of G of around .05%, and therefore my prediction does not contradict experiment, whatever mainstream physicists may assert without thinking.
November 11, 2022 at 8:08 am |
There is an obituary for John McKay written by Leonard Soicher in the LMS Newsletter this month (November 2022, pages 43-44), accessible under https://www.lms.ac.uk/publications/lms-newsletter-back-issues. This mentions a third “coincidence” found by McKay, namely the McKay Conjecture, relating the number of irreducible complex representations with dimension not divisible by a fixed prime p, of a finite group, to the same number for the normaliser of a Sylow p-subgroup. Whole books have been written on this conjecture, and it has been “nearly” proved for many years. I contributed a small part by checking the conjecture for the 26 sporadic simple groups.