I think I may be starting to understand why physicists get so fed up with “crackpots” trying to get their attention. It seems that I have created a sufficient illusion of being a “physicist” myself, that I am starting to get a steady stream of “crackpot” emails. Usually, I try to respond, but this is rarely a productive activity. Mainly, I do not understand what these people are trying to do, and I do not understand why they think I can help them. Therefore, I do not categorise them as “crackpots”, because my failure to understand them does not automatically put them in that category. But it does mean that I am unlikely to be able to help them.
A recent example asked me for a “17-element group”, which taken literally in standard mathematical language means the cyclic group of order 17, but this clearly was not what my correspondent wanted, because his reference point was “Dirac’s 5-element group (Called U(1)*SU(2)*SU(2))”. So what does he mean by “element”? I don’t know, because he didn’t explain when I asked, but it could plausibly mean “element of a basis of a representation”. Which representation? I don’t know, perhaps we have a choice. Clearly it doesn’t have to be an irreducible representation, since in the above “Dirac” case it isn’t. Or perhaps it means a “generator”? But then “Dirac’s group” only needs 2 generators, not 5, so that doesn’t make sense either. So at this stage there is not enough information left to formulate a meaningful question at all. At this point a professional mathematician has no choice but to say, you have to specify your question more precisely, otherwise it does not have an answer.
Well, I tried. It didn’t work.
BUT, I would like to try to draw a lesson from this, and to try to understand why physicists are so resistant to real group theory. I do not know how many physicists would understand the idea that “Dirac’s 5-element group” is U(1)*SU(2)*SU(2), but actually I do understand this, because it does make sense as the group generated by 5 elements that all square to -1 and all anticommute with each other. This is the group generated by the Dirac matrices, and is absolutely central to quantum mechanics. When my correspondent describes it as a “5-element group”, I do understand it, but it is *not* U(1)*SU(2)*SU(2). It is what a group-theorist would describe as a 5-generator group, not a 5-element group, and depending on what exactly you want to do with it, there are quite a number of ways of interpreting “generator” and “group”, and I have written a number of papers about this very issue.
The Dirac group requires five generators, exactly as my correspondent said. As a finite group, it is a central (i.e. tensor) product of Z_4 with two copies of Q_8. It is possible to interpret these generators as generators for a Lie group, but the Lie group you obtain depends on which generators you choose. It is possible to obtain U(1)*SU(2)*SU(2), but it is also possible to obtain a variety of other groups, which, if they are compact, are subgroups of SU(4), but they are not necessarily compact, so could be anywhere inside SL(4,C).
Well, the way I see it, in order to obtain a group-theoretical basis for fundamental physics, it is necessary to extend the “5-element Dirac group” to 6 elements. My correspondent suggests 17 elements. I fail to see why it is necessary to go to such extreme lengths, and he failed to explain it to me. In particular, I have no idea what these 17 elements are supposed to mean physically. I have enough difficulty trying to understand what 6 Dirac matrices mean physically. But I can see that 6 Dirac matrices are sufficient to encapsulate all the physics that I understand. Maybe I don’t understand enough physics, but my impression is rather that the problem is that perhaps physicists do not understand enough mathematics.
March 16, 2024 at 7:28 am |
The label “crackpot” says more about the labeler than the labeled.
March 16, 2024 at 8:19 am |
Crackpottery is in the eye of the beholder.
March 16, 2024 at 8:20 am |
Or should that be:
Crackpottery is in the mind of the beholder.
March 16, 2024 at 10:08 am |
“I don’t know who proposed this view of the Maybe I don’t understand enough physics, but my impression is rather that the problem is that perhaps physicists do not understand enough mathematics.”
The mathematics is the physics itself, in any “theory” where there is no mechanism, just empirical equations based on data. Surely, this is true of most basic physics.
A classical example of Balmer’s 1885 empirical formula for the wavelengths found in hydrogen line spectra. Bohr eventually “explained” Balmer’s formula using his mathematical model of the atom, in which electrons have an energy of 13.6/n^2 electron volts, where n is an integer corresponding to a quantized orbit. Bohr’s “explanation” was then famously attacked by Rutherford who pointed out that Bohr had not proposed any mechanism for discrete orbits so that when a photon was omitted with energy E (causing the electron to lose E of its orbital kinetic energy, and thus spiral inwards) the electrons would “not know when to stop emitting radiation”. Bohr then invented “correspondence” and “complementarity” principles to defend himself. Even now, basic physics is an assembly of half-baked empirical equations, backed up by practical philosophy like “if the boots fit, wear them”. The boots are OK for short walks, but are uncomfortable for long marches.
March 16, 2024 at 10:37 am |
I don’t know the maths/physics background (if any) to the discussion referred to about the Dirac equation in this post. One option is to try to find anomalies and errors in standard theories and correct them in such a way , i.e. a minimalistic correction to orthodoxy.
Dirac’s Hamiltonian energy equation for electrodynamics yields the three SU(2) type gamma matrices, closely related to Pauli’s SU(2) spin matrices. There are two questions to ask physically here.
First, is fermion (spin-1/2 interaction) electrodynamics an SU(2) symmetry theory, rather than the presumed U(1) Abelian theory? If so, can this SU(2) be unified with the weak force’s SU(2) symmetry, rather than having the usual standard model electroweak U(1) X SU(2)?
Second, and even deeper, if you look at the physical (or mathematical if you prefer) basis for Dirac, the energy Hamiltonian he started with the Klein-Gordon version of Einstein’s energy relationship
E^2 = p^2 + m^2 (for mass in energy units, like Mev).
This looks simple but is horrendous to understand physically and mathematically:
E = +/- (p^2 + m^2)^{1/2}
which Dirac rejected, choosing instead
E = {alpha} p + {beta} m
where {alpha} and {beta} are the Dirac matrices.
My approach would be to understand the energy of spin of fermions in terms of the Klein-Gordon equation, in other words look for the mechanism.
March 16, 2024 at 10:56 am |
Yes, there are a lot of difficult puzzles in this area. My approach has been (at least in part) to try and figure out what is “wrong” with the Dirac equation. What is “wrong” with it is chiefly the fact that it does not have a “generation” symmetry to model the three generations of electrons (not to mention the colours of the quarks!). So I’ve tried a number of ways of putting a (discrete) generation symmetry into the Dirac equation. The basic idea is to extend from complex numbers (one imaginary mass term) to quaternions (three imaginary mass terms), but the details are tricky to work out, and I’ve proposed a number of different versions.
As for “mechanisms”, the neutrinos must be involved, and neutrino oscillation must be a crucial mechanism in understanding how the masses of the three generations of electrons are generated, because it is the energy of the neutrinos/antineutrinos that gets converted into/out of electron (and/or quark) mass in the weak interaction.
But I do not buy the standard assumption that neutrino oscillations are “caused” by a difference in mass that is so small it can’t be measured. This assumption is based on the belief that we understand mass better than we understand neutrino oscillations. I contend that we understand neutrino oscillations better than we understand mass, and that therefore this “explanation” puts the cart before the horse, and therefore explains precisely nothing.
March 16, 2024 at 11:44 am |
“My approach has been (at least in part) to try and figure out what is “wrong” with the Dirac equation. What is “wrong” with it is chiefly the fact that it does not have a “generation” symmetry to model the three generations of electrons (not to mention the colours of the quarks!)…. As for “mechanisms”, the neutrinos must be involved, and neutrino oscillation must be a crucial mechanism in understanding how the masses of the three generations of electrons are generated, because it is the energy of the neutrinos/antineutrinos that gets converted into/out of electron (and/or quark) mass in the weak interaction.” – R Wilson
I do have a suggestion about the technical approach to the methematics to correct this: forget Dirac’s approach which is to find a linear solution to Klein-Gordon’s or Einstein’s energy Hamiltonian, H^2 = p^2 + m^2 with gamma matrics. Instead, replace that Hamiltonian with the Laplace transform of the correct overall force field’s potential energy. E.g. Coulomb’s force field has energy density (in standard simplified units) of V = 1/r
To convert this into a hamiltonian, you do a Laplace transform to produce a propagator, 1/(m + k)^2, the denominator of which is apparently the corrected Hamiltonian (the calculation includes an exponential term which allows for vacuum polarization shielding of the Coulomb field), see p1 of my paper https://vixra.org/pdf/1408.0151v1.pdf (using Laplace transforms instead of Fourier avoids the mathematical obfuscation of complex poles in the integral).
The point is, the correct Hamiltonian energy, derived not using Einstein or Klein-Gordon, but derived instead from electromagnetism (Coulomb’s law) is (m + k)^2, where k = p = kinetic energy due to momentum, which might lead to very different conclusions than Dirac’s problemmatic linear solution to +/- (p^2 + m^2)^{1/2}.
Further, you could start off not just with Coulomb’s field energy density, but you could add to that the potentials of the weak and strong nuclear field potentials, before doing the Laplace or Fourier transform to get a combined fields propagator and a full force field. There are various issues here, because of symmetry breaking as a function of energy, the Higgs field mechanism.
March 16, 2024 at 11:55 am |
To clarify, Einstein’s and Klein-Gordon Hamiltonian, p^2 + m^2, leads to Dirac’s gamma matrices. By contrast, the Laplace transform of the Coulomb field, 4π ∫ r exp[-r(m + p)] = 1/(m + p )^2, the correct Coulomb field propagator, suggests that m^2 + 2km + k^2 is the true basis for finding gamma matrics, rather than p^2 + m^2 as Dirac assumed.
March 16, 2024 at 11:56 am |
p=k
March 19, 2024 at 7:38 am |
There may well be something important in these remarks. But I do get nervous when momentum is treated as a scalar rather than a vector, so that I don’t really know how to interpret a formula like (m+p)^2. Sometimes I implement m as a vector, which allows me to interpret (m+p).(m+p) as a scalar product, but scares the shit out of people because I am linking the three generations of electrons to three directions of the gravitational field. More often I combine scalars and vectors into quaternions, which avoids that particular problem but creates others.
But I feel the problems with the Dirac equation go even deeper. Dirac starts from Einstein’s m = sqrt{E^2-p^2}, and re-arranges it as -m^2 = p^2-E^2. Then he wants to factorise the right-hand side as (p+E)(p-E), but this doesn’t make sense as it stands, so he introduces the gamma matrices so that it does make sense. But he still has anti-particles with negative energy. To avoid negative mass as well, he factorises the left-hand side as (im)^2, which actually makes matters worse because it makes the mass imaginary.
On the other hand, if we follow Hamilton rather than Lagrange, we should write the equation as E^2=m^2+p^2, and write m+p as a quaternion q=m+ip_1+jp_2+kp_3, so that the right-hand side factorises as q.bar{q}. Now we want to factorise the equation into particles E=q and anti-particles E=qbar, so that anti-particles have positive energy and positive mass (as experiment tells us). Again we need to introduce more quaternions (i.e. the spinors) into the equations in order for them to make sense, but we do not need the gamma matrices.
This makes everything much simpler than in Dirac’s version. Anti-particles have opposite parity to the particles, but they do not travel backwards in time. Local spacetime symmetries become Euclidean SO(4), as required by QM, rather than Lorentzian SO(3,1). Instead of requiring SL(2,C)=Spin(3,1) to describe spinors, or Spin(4) = SU(2) x SU(2), we can identify spinors as Euclidean spacetime vectors. Of course, spinors are not the same as Minkowski spacetime vectors, as everybody knows.
Finally, this avoids the problem that there is no thing as a generally covariant spinor, which is one of the major problems with combining particle physics with gravity. We do not need spinors, which is just as well, because they don’t exist in the real world.
March 21, 2024 at 2:52 am
I wondering how you feel about Geometric Algebra where adding scalars and vectors is a feature not a bug?
Also what textbook would you recommend to gain a good solid footing in finite group theory?
March 21, 2024 at 7:23 am
That wikipedia reference equates “geometric algebra” with “Clifford algebra”, although I would say that “geometric algebra” is a somewhat more general concept. Geometric algebra is a good way of formalising what physicists actually do, in order to make it more rigorous.
But it is really just a generalisation of quaternions – which is the even part of the Clifford algebra of ordinary Euclidean 3-space, with negative definite signature. With positive definite signature, one gets the split quaternions instead. The full Clifford algebra (negative definite case Cl(0,3)) is the sum of two copies of the quaternions, and is, in my opinion, the correct place to formalise electromagnetism (by which I mean quantum electrodynamics).
My point is that it is necessary to do algebra not just in the quaternions, but over the quaternions – that is, one needs matrices whose entries are quaternions. That is not done in ordinary geometric algebra. However, it is done in non-commutative geometry, which is why sophisticated attacks on quantum gravity use non-commutative geometry.
So what I am doing is effectively non-commutative geometry, but in a flat spacetime, not on an arbitrary manifold. You might say that I am doing non-commutative Euclidean geometry, rather than non-commutative (pseudo-)Riemannian geometry. Instead of working with a complex 4-dimensional spacetime, as the standard Dirac formalism does, I work with a quaternionic 4-dimensional spacetime, whose real part is classical spacetime, and whose imaginary part is all the matter and stuff that lives in spacetime.
Quaternionic symmetries then act to convert spacetime into matter, and matter into spacetime (creation and annihilation operators), so that they describe the quantum vacuum. The group here is Sp(4), which is a compact 21-dimensional group. General relativity is an attempt to use the non-compact 15-dimensional group SL(4,R) instead. It works for small perturbations of classical physics, but not in general, because it only has 12 non-classical degrees of freedom, rather than 18. And because it is not compact, it creates singularities, which are impossible in a proper compact quantum theory.
March 21, 2024 at 7:33 am
Oops, sorry, Sp(4) is 36-dimensional. The 21-dimensional group is Sp(3). I am not sure which is the “correct” group to use here, but I am inclined to think it might be Sp(3), since that group distinguishes time from space, or perhaps Sp(1) x Sp(3), so that real time can be dilated, and real space can be contracted, without having to mix space with time.
March 21, 2024 at 8:23 am
There is a problem with the interpretation of time dilation and length contraction that I am not sure is well enough appreciated – that is the question of whether they are physically real effects, or merely exist in the eye of the beholder. When challenged, physicists will usually (but not always) agree that they are not physically real, and they merely reflect different observers’ measurements of one physical reality. The problem then is to assign actual numbers to the “physical reality” that underlies space and time measurements. Whose measurements do we take as definitive? Or do we abstract a theoretical absolute time from all possible measurements? Or do we just work with an infinite set of possible measurements?
I don’t believe these questions have ever been satisfactorily answered, because definitions used in physics are always circular. Time cannot be defined at a point, because it always depends on the environment. Time itself is a non-local concept. This is even more obvious in General Relativity, where time also depends on the gravitational field, which is itself a non-local concept. So again, one has to ask the question, is the “curvature of spacetime”, that GR implies, physically real, or merely “in the eye of the beholder”, that is, a feature of the measurement, not a feature of the underlying physical reality?
Die-hard relativists will, if you are not careful, insist that it is physically real. But astronomy and cosmology demonstrate pretty convincingly that spacetime is very flat on very large scales. The curvature is not physically real. Therefore one should not base a model of physical reality on a curved spacetime manifold. One should base it on a flat spacetime. One should distinguish between physical reality, and measurements of reality. It is truly amazing how many physicists confuse their own measurements of reality with the reality itself.
One has to bite the bullet, and admit that physically real space does not contract or bend or twist or curve, and physically real time does not dilate. If a clock runs slower or faster according to the gravitational field, that does not mean that time itself is different, it means that the measurements of time are different, and need to be re-calibrated. That is of course what physicists actually do in practice: they use General Relativity to tell them how to re-calibrate their clocks.
But the philosophical consequences are profound: the running of an atomic clock, using electromagnetic properties of atoms, is not independent of the gravitational field. This shouldn’t come as a surprise to anyone, because we know that photons follow curved paths in a gravitational field, so that electromagnetism and gravity do mix. Why therefore do we insist on defining time using electromagnetism only, and not gravity? It is obvious that such a procedure will produce inconsistent results, and inconsistent theories. We must accept that gravity mixes with the other forces, or else unification is impossible. Worse, a consistent definition of spacetime is impossible.
March 19, 2024 at 12:21 pm |
Thank you for the clear summary of what you’re doing.
March 20, 2024 at 7:26 am |
There is another aspect to Dirac’s negation of m^2=E^2-p^2, which is that physicists define the Lie bracket (for the Lie algebra of spacetime derivatives) as [A,B]:=i.hbar.(AB-BA), rather than the mathematicians’ definition [A,B]:=AB-BA. The factor of hbar is just a distraction, used for quantising the Lie algebra, but Lie algebras are automatically quantised, so we might as well put hbar=1. This allows us to use Lie algebras for things other than angular momentum/spin, and put in the appropriate units afterwards.
But the factor of i is insidious, because it only allows physicists to use complex Lie algebras, never real or quaternionic Lie algebras. The reason is that this factor of i converts mathematicians’ anti-Hermitian matrices into physicists’ Hermitian matrices, but this only works in the complex case, where there are n^2 independent matrices in both the Hermitian and anti-Hermitian cases. In the real case, there are n(n+1)/2 independent Hermitian (symmetric) matrices, but only n(n-1)/2 anti-Hermitian (anti-symmetric). In the quaternionic case, there are n(2n-1) Hermitian and n(2n+1) anti-Hermitian.
In order to model three generations of electrons, it is necessary to use a quaternionic Lie algebra, which means extending the complex Pauli matrices to quaternionic. Now there are 6 independent Hermitian matrices, and 10 independent anti-Hermitian. The Hermitian ones do not form a Lie algebra, so do not model differential equations, and do not quantise anything. The anti-Hermitian ones do form a Lie algebra, which happens to be so(5), in case anyone is interested. You can find an isomorphic copy of it inside the Dirac algebra by taking generators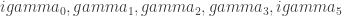 .
.
Now we can ask, what does this Lie algebra quantise? Well, it’s basically the same as the Dirac equation, that is a quantisation of the Einstein mass equation, so what it quantises is mass. It needs re-arranging a bit, inside a quaternionic (rather than complex) Dirac algebra, in order to separate the electron generation from the direction of spin, but after that there are five fundamental masses quantised by this Lie algebra, namely the three generations of electron, plus the proton and neutron.
If it quantises mass, then it quantises gravity. The 5-dimensional representation of so(5) is reminiscent of the “spin 2 graviton” that comes out of GR, and the 10-dimensional (adjoint) representation, that should contain the gauge bosons, matches the 10 dimensions of the Einstein field equations (i.e. the 10 dimensions of the stress-energy tensor and the Ricci tensor). But it doesn’t match properly, because Einstein uses so(3,1) instead of so(5). Kaluza-Klein gets closer, but still hasn’t got the quaternionic structure right. Dirac, of course, identifies so(3,1) with sl(2,C), which requires both the Hermitian and anti-Hermitian versions of the Pauli matrices, so we need to do the same in the quaternionic case, which gives us the Lie algebra sl(2,H) = so(5,1). Now we at least have a chance that it might work.
March 21, 2024 at 9:51 am |
Another comment about geometric algebra that is also relevant to the next post (Hermitian or anti-Hermitian) is the fact that in general the Clifford algebras Cl(p,q) and Cl(q,p) are not isomorphism. This is one of the great puzzles about the Dirac algebra: why does it need to combine both Cl(1,3)=M_2(H) and Cl(3,1)=M_4(R) into a single algebra M_4(C)?
Extending to the conformal group, and extending spinors to twistors, we can ask about the distinction between Cl(2,4)=M_4(H) and Cl(4,2)=M_8(R). Peter Woit uses M_8(R) to combine his left-handed and right-handed twistors. I use M_4(H). Why do I do this? What is the difference?
The difference is in the signature of the Clifford algebra. Cl(2,4) has signature (28,36) and compact subgroup Sp(4). Cl(4,2) has signature (36,28) and compact subgroup SO(8). Almost no difference in the geometry, but a huge difference in the algebra. Reversing the signature is what happens when you multiply by i, to convert between Hermitian and anti-Hermitian matrices. So you might naively think that it really doesn’t make much difference. But you’d be wrong.
Most people in the GUT community work with orthogonal and unitary groups, and/or some of the five exceptional groups. They rarely, if ever, consider the symplectic groups. I don’t understand why they do this. They would much rather embed SU(3) in SO(8), via SU(4) and/or SO(6), than embed it in Sp(4), via SU(4) and/or Sp(3). They are obsessed with SO(8), because it is generated by octonions, and they think that because SU(2) comes from quaternions, SU(3) must come from octonions. Unfortunately, it doesn’t, at least not without a struggle. They struggle, and they force the Standard Model into an octonionic mould, but it does nothing for them. It tells them nothing new about physics.
The number 28 in the two cases refers to (a) the number of independent Hermitian 4×4 quaternion matrices, and (b) the number of independent anti-Hermitian 8×8 real matrices. The number 36 in the two cases refers to (c) the number of independent Hermitian 8×8 real matrices, and (d) the number of independent anti-Hermitian 4×4 quaternion matrices. Now the anti-Hermitian cases (b) and (d) generate Lie algebras, so(8) and sp(4) respectively. The Hermitian cases (a) and (c) generate coset spaces gl(4,H)/sp(4) and gl(8,R)/so(8) respectively. If you just do numerology, and try to relate the two 28s to each other, or the two 36s to each other, you get nonsense.
The two 36s are sp(4) and gl(8,R)/so(8). The one that relates to physics in 4-dimensional spacetime is sp(4), which represents the unified gauge group of quantum physics, including quantum gravity. To get the Standard Model gauge algebra from this, you take the representation on 4-dimensional quaternions, split off the real part to call spacetime, then split space from time so that you are left with 3-dimensional imaginary time (called su(2)) plus 9-dimensional imaginary space (called u(3) = u(1)+su(3)).
The two 28s are so(8) and gl(4,H)/sp(4). The one that relates to physics is the coset space gl(4,H)/sp(4), which describes how classical physics works when you ignore the gauge group sp(4) of the entirety of quantum physics. To unify the classical and quantum approaches, just take the algebra gl(4,H), which contains everything at once.
The ones that do not relate to physics are so(8) and gl(8,R)/so(8). It is impossible to embed the SM gauge algebra u(1)+su(2)+su(3) in so(8), and it is impossible to define a 4-dimensional spacetime in the coset space gl(8,R)/so(8). Why is everybody obsessed with using so(8) to describe physics? It can’t be done. Octonions, E8 GUTs, E8 x E8 heterotic string theory, they are all different aspects of the obsession with so(8), and they all fail to capture any useful aspect of physical reality.
If you want to unify quantum physics, classical physics, measurement theory and relativity into a consistent whole, then the only possibility is to use sp(4) for quantum physics, gl(4,H)/sp(4) for classical measurements of quantum phenomena, and gl(4,H) for the unification of everything. This is the only fair game in town. Don’t play the octonion game, or the E8 game, or the string theory game, because those games are rigged, and you will lose everything. Play the gl(4,H) game, and win the Nobel jackpot.